Asignatura: Laboratorio de Redes

Curso: 6° Informática

Profesora: Evangelina Rivero

Teoría de la Información. Codificación:  redundancia para la detección y corrección de errores

1) Para poder comprender y entender de de que se trata la Teoría de la Información vamos a ver estos vídeos de los cuales vamos a ir tomando nota.

https://www.youtube.com/watch?v=vVokVFHz8uA

https://www.youtube.com/watch?v=af_auu5YX0g

https://www.youtube.com/watch?v=pUsL7vm-xag

https://www.youtube.com/watch?v=gHg8X1Ce32w

Información a extraer: Quién presentó la propuesta sobre la teoría de la información? Concepto de teoría de la información? Qué es un sistema de comunicación? Cómo está compuesto? Cuáles son sus componentes? Qué es la información? Cuáles son fuentes de información? Tipos de información: clasificación y concepto. Qué es la entropía? Tipos de entropías.

2) Del texto de Detección y corrección de errores realizar un breve resumen.

Código de Hamming: Detección y Corrección de errores

Quién iba a decir que fuera un juego -como lo lees un juego- el algoritmo de Hamming, que lo que trata es de corregir errores, sea como un juego de deducción -como el juego del Cluedo o el Sudoku- donde nos dan una serie de pistas iniciales, y necesitamos descubrir quién es el malo o que número va en cada posición por descarte.

Parece un sueño que si enviamos unos bits (una imagen, un audio, un texto, lo que sea) por Internet. Cuando llegue a su destino, y llegue mal (bits cambiados aleatoriamente; donde antes había un “1” ahora un “0”, y viceversa) por alguna causa -como una tormenta electromagnética por el camino entre el ordenador que lo envía y el que lo recibe- podamos corregir los errores que han ocurrido por el camino en el destino.

Este algoritmo es, por así decirlo, un juego de detectives. Donde tenemos varias personas (los bits), y hay uno, varios o ningún malo (bits erróneos) entre ellas. A su vez tenemos varias pistas que van a hacer que descartemos a los buenos, hasta quedarnos con los malos; aunque ojo, también puede haber pistas que mientan. Realmente es bastante sencillo.

Es decir, hay unos bits que corrigen a otros. Estos bits que corrigen a otros se llaman “bits de redundancia”, pues son bits extra a la información para intentar corregir los errores o al menos comprobar que todo esté correcto. Un ejemplo en el mundo físico, sería como tener en un papel un texto cualquiera como “Mi mamá me mima”, y más abajo en el mismo papel la suma de todas las letras del texto “M=6, I=2, A=3, E=1” (es información repetida/redundante, pues ya está contenido en el dato). De este modo si se nos cae líquido encima de la tinta del texto haciendo ilegible algunas palabras del texto “Xi XaXá me Xima” (las “X” representan la ilegibilidad del texto); todavía podemos recuperar el texto original con la suma de letras pues sabemos que hay 6 “Ms” y solo vemos legibles 2, por lo que se deduce que las letras ilegibles tienen que ser “Ms” también (lo mismo ocurriría si las equis “X” anteriores fueran letras y no borrones, la letra equis “X” no existe en las letras sumadas por lo que es una letra errónea). Al dato original más los “bits de redundancia” se les conoce como “Bloque del código” (en inglés “Block Code”).

La “distancia mínima de Hamming” es muy interesante para corregir errores en bits (más información en el artículo de Hamming; te recomiendo que lo leas a continuación de éste artículo). Realmente sirve para corregir cualquier tipo de fichero (audio, imagen, etc) en informática, pues los bits son la base de cualquier fichero, y si los bits están correctos pues el fichero debería de estar correcto (debería, pues si, por ejemplo, con un ataque “man in the middle”, un tercero modifica el fichero por el camino del fichero durante el envío; este método corregirá los errores del fichero si llegan mal al destino entre el tercero y el destino, pero no detecta si el contenido ha sido modificado deliberadamente).

Código Hamming

Para empezar con cualquier juego necesitamos unas normas. Y las normas de Hamming son las tres siguientes (si estas instrucciones no te aclaran mira la imagen que viene después, y luego vuelve, lo vas a entender enseguida):

1. Utilizaremos como “bits de redundancia” los conocidos como “bits de paridad” para comprobar si hay errores o no (serán las pistas): “1” significa “impar”, y “0” significa “par” (el «Bit de Paridad» es la suma de “1s”; por ejemplo, la cadena de bits “1011” la suma de “1s” es 3, que es impar, por lo que el bit de paridad es “1”, Si tienes curiosidad tienes más información sobre «bits de Paridad» en este otro artículo sobre «Dígitos de control» haciendo click aquí).
2. Cada “bit de paridad” comprobará unos bits determinados, dependiendo de la posición que ocupe y siguiendo las normas del siguiente ejemplo. Por ejemplo, la posición es 4, desde está misma posición se seleccionarán 4, luego dejará 4 sin seleccionar, seleccionará los siguientes 4, para luego dejar los siguientes 4 sin seleccionar, y así hasta el infinito. Lo mismo para todas las posiciones que son potencias de dos (para la posición 1 es uno sí, uno no, uno sí, uno no, etc; ¿Y para la posición 2? Dos sí, dos no, dos sí, dos no; la cuatro te la he dicho antes, ¿Y para los siguientes 8, 16, 32, etc? es muy fácil).
3. De las anteriores selecciones el “bit de paridad” es de lo seleccionado la posición de número más pequeña (evidentemente, porque si el bit de paridad dice si es par o impar la suma de los “1s”, si se comprobara a sí mismo, entraríamos en un bucle infinito sin sentido), el resto son los bits que comprueba (que serán los que se sumen para saber si es par o impar).

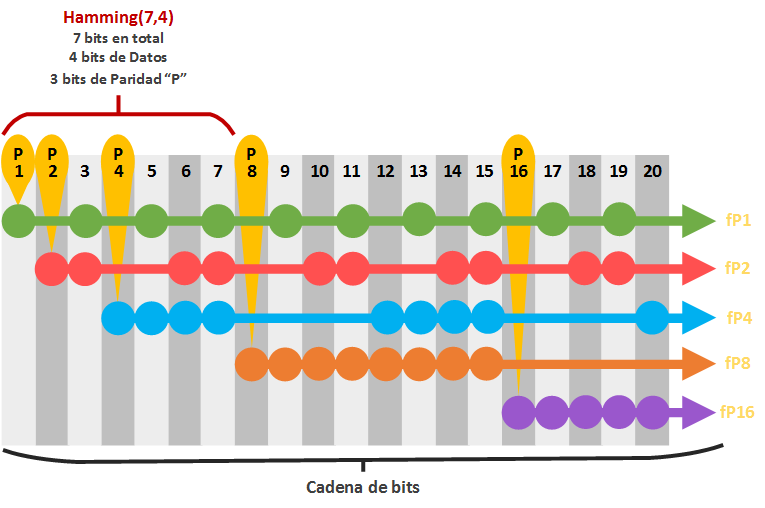
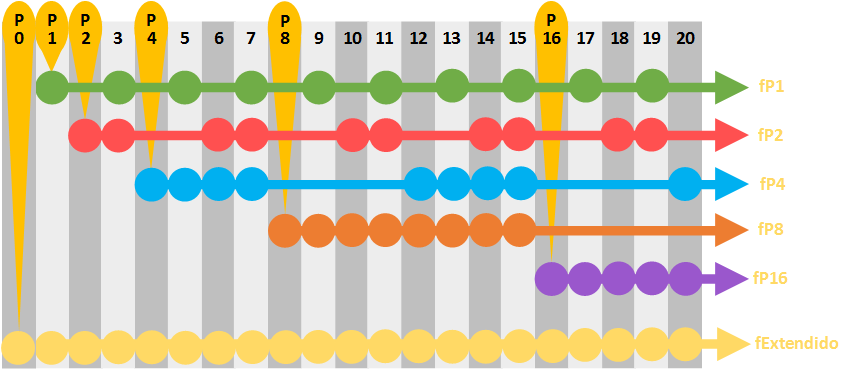
Siguiendo estas instrucciones podríamos dibujar hasta el infinito una matriz infinita. Pero vamos a reducirla hasta la posición 20 que puedes ver en la siguiente imagen (el resto hasta el infinito es igual 😉 ).

Verás que la cadena de bits se compone de bits de datos y bits de paridad mezclados (pero no revueltos 😉 ). Sabemos que los bits de paridad son las potencias de dos: 1, 2, 4, 8, 16 (el siguiente es 32, y el ejemplo solo tiene 20 bits, así que ya paro la cuenta). Al “bit de paridad” en sí lo he llamado en la imagen “P” seguido de la posición que ocupa (por ejemplo, el que ocupa la posición 4, lo he llamado “P4”). No hay que confundir con las filas de bits que comprueba cada “bit de paridad” e incluyéndose así mismo; a cada fila de éstas la he denominado en la imagen como “fP” seguido de la posición en la que empieza (como “fP4”, que es la fila que comprueba el “bit de paridad” llamado “P4” e incluyéndose así mismo). Esto es una matriz vulgar y corriente, lo único que un poco más emocionante. Esta matriz se llama “Matriz de comprobación de paridad” (Parity-check Matrix) o “Matriz Síndrome” (Syndrome Matrix); a esta matriz a mí me gusta llamarla “Matriz de deducción” que suena mucho más misterioso y porque esta matriz nos servirá para deducir con las pistas los bits que están mal para poder corregirlos, o simplemente detectar si hay errores.

Seguro que te has fijado en que encima de la “matriz síndrome” anterior aparece la palabra “Hamming(7,4)”. Lo he querido señalar porque es el código Hamming más típico. Aunque existen infinitos, pero siempre siguiendo las normas, otros podrían ser el:

• Hamming(3,1)
• Hamming(15,11): en la matriz de la anterior imagen llegaría justo hasta antes de la posición 16
• Hamming(31,26): llegaría justo hasta la posición anterior a la 32
• etc…

Centrémonos en “Hamming(7,4)”, que quiere decir que por cada 7 bits que representan datos hay 4 que son bits de Datos y los (7 – 4 =) 3 restantes son “bits paridad”. Dicho de otro modo, si dividimos en cachos de 4 bits un vídeo/foto/audio/texto; obtendríamos, por ejemplo, un trozo que podría ser “1011”.

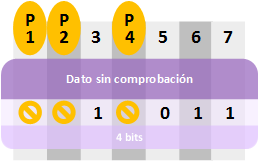
A este cacho de 4 bits se le añaden 3 bits más que servirían para comprobar los datos (los “bits de paridad”). Para ello los ubicamos reservando los huecos para los “bits de paridad” de las posiciones 1, 2 y 4 (como en la “matriz síndrome” que vimos más arriba).

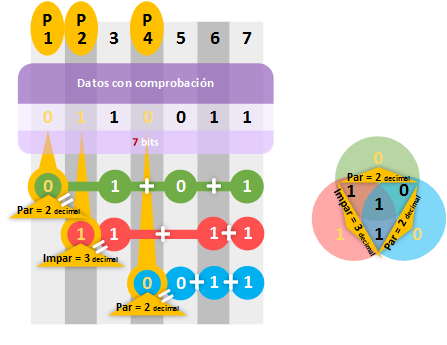
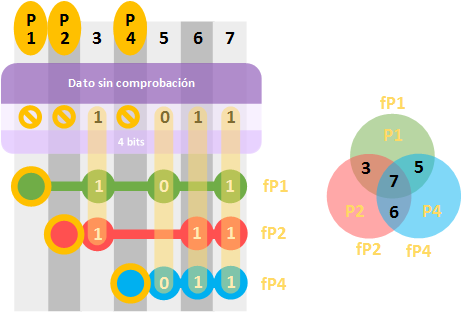
Completamos las filas que comprobarán cada “bit de deducción” en la “matriz síndrome” (hasta la posición 7, no necesitamos más) con las normas antes descritas. Como puedes ver en la imagen siguiente (te recomiendo que ojees a la imagen siguiente a medida que lees este párrafo), tenemos 3 filas: “fP1”, “fP2” y “fP4”. Estas filas se pueden representar igualmente por conjuntos (pues cada fila contiene un conjunto/grupo de bits), y podemos ver que hay bits en algunas filas que comparten la misma posición (no confundas el “bit de paridad” como “P4”, con la fila que comprueba “fP4” en la que se incluye el propio “P4”, así como los datos de las posiciones 5, 6 y 7; así que nunca coincidirán las posiciones de los “bits de paridad”, pero sí de los bits que comprueba y esto veremos más adelante porqué es). De este modo, vemos que son conjuntos que represento con los mismos colores (o mismo “fP”) tanto en fila (en la imagen la “matriz síndrome” al a izquierda) como en círculo (en la imagen los círculos de colores):

• fP1 o Verde: con el “bit de paridad” P1, y las posiciones de datos 3, 5 y 7
• fP2 o Rojo: con el “bit de paridad” P2, y las posiciones de datos 3, 6 y 7
• fP4 o Azul: con el “bit de paridad” P4, y las posiciones de datos 5, 6 y 7

Solo nos queda calcular los “bits de paridad”. Simplemente sumamos los “1s” de cada fila, miramos si es par o impar (recordatorio: “par” = ”0”, e “impar” = “1”), y completamos el “bit de paridad”. En los conjuntos circulares he cambiado las posiciones de la anterior imagen por los bits propiamente.

Ya tenemos la cadena de bits que incluye los datos y los “bits de comprobación” siguiendo “Hammin(7,4)”.

Nombres de los grupos de bits

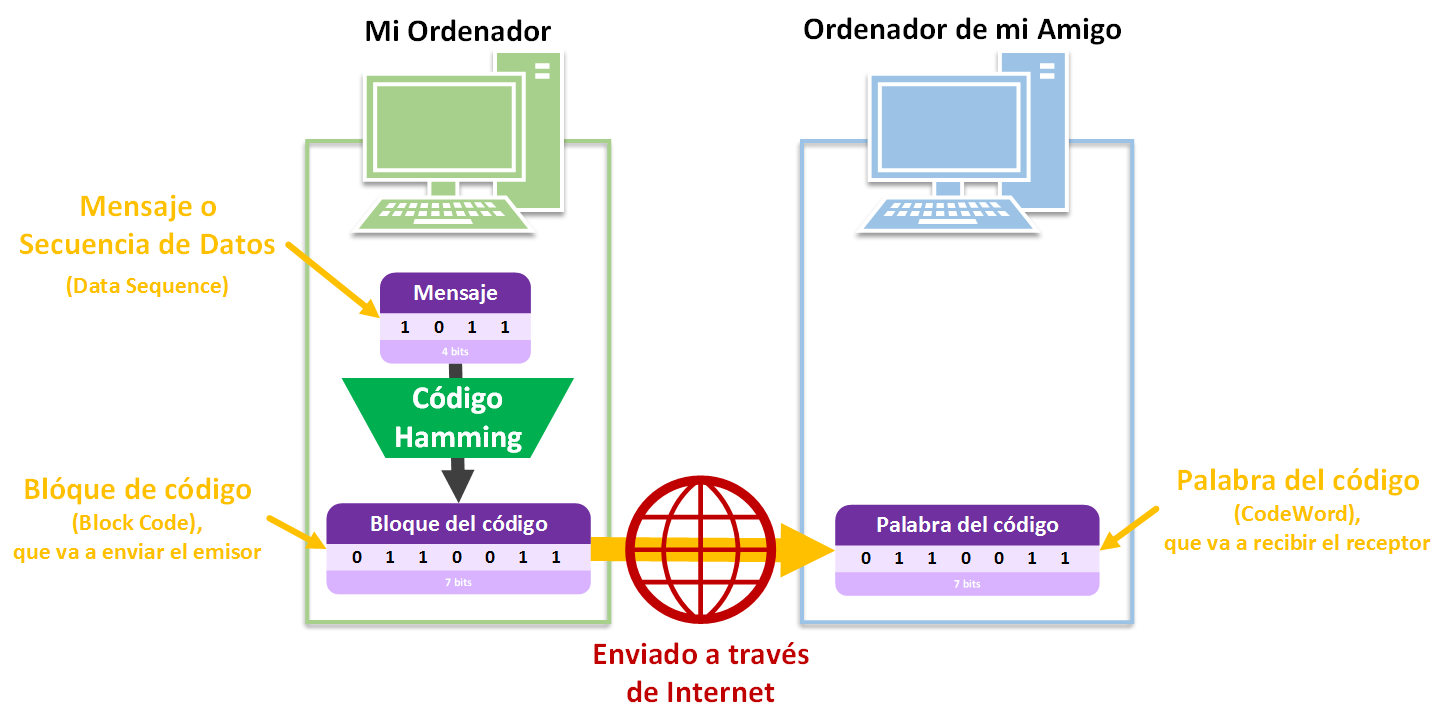
No he querido poner nombres nuevos durante la explicación para no complicar la explicación (y continuaré sin hacerlo un buen rato para que la lectura del artículo sea armoniosa). Realmente al dato que se envía se llama “Mensaje” o “Secuencia de Datos”, que se convierte mediante el “Código de Hamming” a un “Bloque de código”.

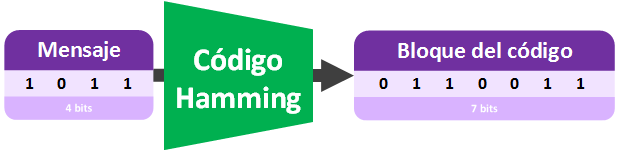Si queremos enviar el “Bloque de código” por Internet al ordenador de, por ejemplo, un amigo, ya no se llamará “Bloque de código” sino que se llamará “Palabra del código”, pues se preparará (añadiendo otros bits con significado, cuyo significado dependerá del protocolo de la comunicación) para entrar en un canal de comunicación que es Internet.

Resumen de las palabras:

• “Mensaje” o “Secuencia de Datos” (en inglés, “Data Sequence”): normalmente el trozo de lo queremos enviar (por ejemplo, un fichero grande, dividido en pequeños trozos que son los mensajes)
• “Bloque del código” (“Block Code”): Por teoría de la codificación, el resultado de aplicar un codificador (como el código Hamming) al mensaje para que le añada bits de redundancia (como los bits de paridad). (Nota sobre la traducción: No traduzco «Block Code» a «Código del Bloque» y sí a «Bloque del código», pues un «Código corrector de errores» codifica los datos en bloques, por lo que uno de estos bloques pertenece a un «Código» que lo ha creado, y podemos decir que es un «Bloque del código»)
• “Palabra del código” (“Code Word”): Por teoría de la comunicación, lo que queremos enviar por un canal de comunicación (como Internet), que normalmente va a ser un “Bloque de código” para corregir errores quien reciba la “Palabra del código” (Podría ser también un “Mensaje” la “Palabra del código”, aunque si llegan bits erróneos al receptor no habrá forma de corregirlos al no tener bits de redundancia).

Buscar errores y corregirlos

Ahora lo mismo, pero al revés ¡Que dé comienzo el juego de deducción!

Supongamos que nos llega por Internet (o un dato de un disco duro) la siguiente cadena de bits, con bits de datos y “bits de paridad”. Tenemos que comprobar que esté bien el dato antes de utilizarlo; no vaya a ser que por Internet debido a alguna interferencia se haya cambiado algún bit (o si estuviera en nuestro disco duro de plato, pudiera ser que se haya desmagnetizado algún bit; para los discos duros SSD podría ser que alguna celda de memoria estuviera defectuosa y no guardara bien algún bit, por ejemplo). Vamos, que queremos utilizar la siguiente cadena de bits y no sabemos si está correcto para poder utilizarlo ¡Comprobémoslo!

No sabemos si tiene algún error o no, puede que esté correcto, puede que tenga algunos bits cambiados; tampoco sabemos si los que están mal son los bits que corresponden con los datos o los propios “bits de paridad” ¿Entonces, si está mal algún “bit de paridad” ya no podremos corregir o comprobar nada? También podemos saber si está mal algún “bit de paridad” e incluso corregirlo, veamos cómo.

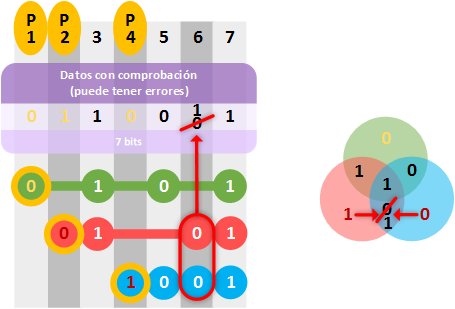
Lo primero que tenemos que hacer es rellenar la “matriz síndrome”. No rellenamos los “bits de paridad”, pues es lo que utilizamos para realizar las comprobaciones; es lo que tenemos que volver a calcular igual que antes.

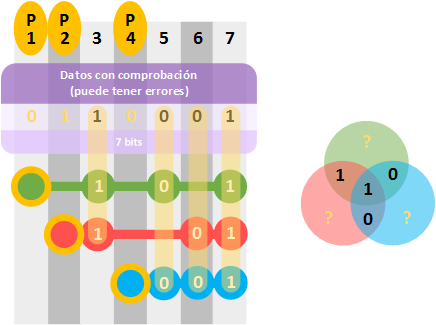Al igual que hicimos anteriormente calculamos los “bits de paridad”. Una vez calculados comprobamos con los que ya tenía la cadena entera, miramos si coinciden.

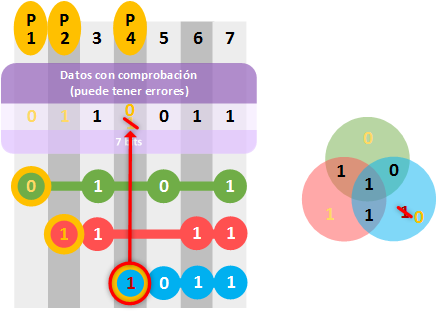
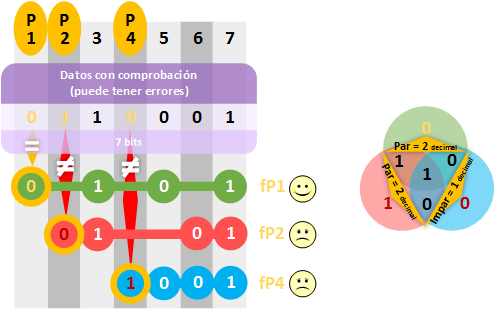En el ejemplo podemos comprobar que hay 2 “bits de paridad” que no coinciden en las filas “fP2” (rojo) y “fP4” (azul), con lo que hay algo mal seguro. Pero, ¿qué bit está mal? Con lo que deducimos que el bit erróneo debe pertenecer a ambas filas (en este juego de deducción, con las pruebas hemos logrado reconocer al malo). Por lo que, si no es “0” el bit erróneo, debe ser “1” y lo corregimos.

¿El bit de la posición 7 no está también coincidiendo en las dos filas marcadas como erróneas? Ten en cuenta que el bit “1” de la posición 7 ya nos está diciendo la fila “fp1” (verde) que está bien. Solo el “0” de la posición 6 coincide con las filas “fP2” (rojo) y “fP4” (azul) únicamente; y es el que está mal.

Una vez corregido podemos quitar los “bits de paridad” y obtener el dato en perfecto estado, así usarlo. Si era un trozo de una imagen, por ejemplo, después de comprobar el resto de cachos y componer todos los bits de la imagen, podemos ya por fin visualizarla sin ningún problema.

¿Y si el que está mal era un “bit de paridad”? Como el siguiente:

Su “matriz síndrome” nos revelará que lo único que está mal es el propio “bit de paridad”. Pues como hemos dicho más arriba, los “bits de paridad” no son coincidentes con bits de otras filas; por lo que si el error lo tiene el “bit de paridad” siempre va a estar en soledad. Sabiendo que está mal podremos corregirlo o no, lo que nos importa es el dato realmente que está correcto.

¿El código de Hamming hasta cuantos bits puede corregir? Evidentemente si todos son erróneos, es imposible corregir nada, pues es otra cosa diferente que se validaría como correcta (Si tenemos una puerta a la que le falta una bisagra la podemos arreglar; lo que no podemos es suponer que una manzana es una puerta en mal estado e intentar “arreglarla” poniéndole una bisagra, pues una manzana es otra cosa, no es una puerta). Para saber cuántos bits se pueden corregir se necesita la “Distancia de Hamming” (la veremos en otro artículo)

Hamming extendido

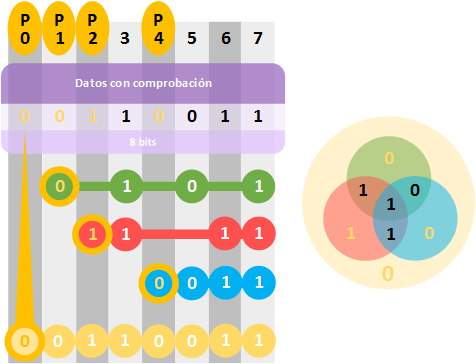
También se utiliza el “Hamming Extendido” para asegurar una mejor detección. Simplemente consiste en añadir una fila adicional completa, y un nuevo bit de paridad en la primera posición.

Nota sobre la Matriz síndrome anterior: La puedes utilizar para practicar código Hamming al imprimirla (en blanco y negro al ser posible) y escribir encima.

Un ejemplo del código Hamming Extendido aplicado con lo antes visto sería:

Para terminar, fíjate bien que ya no sería “Hamming(7,4)”, sino “Hamming(8,4)” (4 bits de datos más 4 bits de paridad).

Asignatura: Laboratorio de Programación III

Curso: 6° Informática

Profesora: Evangelina Rivero

Seguimos trabajando con Pseint!!

1) Continuamos con la función si. En este vídeo veremos una explicación sencilla https://www.youtube.com/watch?time_continue=19&v=9Z2owQA63V0&feature=emb_logo
2) Realizar un breve resumen sobre la función si
3) Realizar los ejercicios en las computadoras y luego copiarlos en sus carpetas: pseudocódigo y diagrama de flujo.

La semana que viene veremos otras funciones. 

Pseudocódigo

4 - Comprobando Condiciones (1: Si)

En casi cualquier secuencia de instrucciones para un ordenador, será vital poder comprobar si se cumple alguna condición. Una primera forma básica de comprobar condiciones es con la orden "SI". Su uso básico sería

Si condicion Entonces
    pasos_a_dar_si_es_verdadero
SiNo
    pasos_a_dar_si_es_falso
FinSi

El bloque "SiNo" es opcional: podemos optar por no indicar lo que queremos que se haga cuando no se cumpla la condición.

Para ayudarnos a planificar el comportamiento de una secuencia de instrucciones, se suele usar como ayuda los llamados "diagramas de flujo". En estos diagramas, una condición se representa como un rombo, del que salen dos flechas: una para la secuencia de acciones a realizar si se cumple la condición y otra para cuando no se cumple:

Así, si en PSeInt hacemos clic en el icono de la parte derecha que representa la condición SI-ENTONCES, aparece un esqueleto de programa casi completo, para que hagamos los cambios que nos interesen:

Sólo tenemos que escribir la condición que realmente nos interesa, y la serie de pasos que se deben dar si se cumple y si no se cumple, de modo que nuestro programa podría quedar así:

Algoritmo Ejemplo004

  Escribir "Dime un numero"
  Leer primerNumero
  Escribir "Dime otro numero"
  Leer segundoNumero

  Si primerNumero > segundoNumero Entonces
    Escribir "El primero es mayor"
  Sino
    Escribir "El segundo es mayor"
  FinSi

FinAlgoritmo

Su resultado sería éste:

(Nota: si lo piensas con un poco de detenimiento -o lo pruebas-, te darás cuenta de que ese planteamiento no es correcto del todo: si introduces dos números iguales, te dirá que el segundo es el mayor; lo solucionaremos un poco más adelante, en el ejemplo 4c).

En ese ejemplo hemos comparado si un valor es mayor que el otro (>). Los operadores de comparación que tenemos disponibles son:

Operador relacional	Significado	Ejemplo
>	Mayor que	3>2
<	Menor que	2<3
=	Igual que	3=3
<=	Menor o igual que	5 <= 5
>=	Mayor o igual que	6 >= 5
<>	Distinto de	6<>5

Ejercicio de repaso propuesto 4.1: Crea un programa que pida dos números al usuario y responda si son iguales o no lo son.

También es posible comprobar varias condiciones a la vez, para hacer construcciones más complejas, como: "si a es mayor que b y b es mayor que c", o como "si a es igual a 1 o b es igual a 1 ". Los operadores lógicos que de los que disponemos son:

Operador lógico	Significado	Ejemplo
& ó Y	Conjunción (y).	(7>4) & (2=1) //falso
| ó O	Disyunción (o).	(1=1 | 2=1) //verdadero
~ ó NO	Negación (no).	~(2<5) //falso

Un ejemplo de su uso sería:

Algoritmo Ejemplo004b

  Escribir "Dime un numero"
  Leer primerNumero

  Si primerNumero > 0  o  primerNumero = 0 Entonces
    Escribir "Es mayor o igual que cero"
  Sino
    Escribir "Es negativo"
  FinSi

FinAlgoritmo

Además, podemos encadenar varias condiciones una detrás de otra. Como hemos comentado, el ejemplo 4 fallaba si los dos números son iguales. Por eso, un planteamiento más detallado (y más correcto) sería emplear dos comprobaciones "si", de la siguiente manera:

Algoritmo Ejemplo004c

    Escribir "Dime un numero"
    Leer primerNumero
    Escribir "Dime otro numero"
    Leer segundoNumero

    Si primerNumero > segundoNumero Entonces
        Escribir "El primero es mayor"
    Sino
        Si primerNumero < segundoNumero Entonces
            Escribir "El segundo es mayor"
        Sino
            Escribir "Son iguales"
        FinSi
    FinSi

FinAlgoritmo

Ejercicio de repaso propuesto 4.2: Haz una variante del ejemplo 004b, usando el operador ">=".

Ejercicio de repaso propuesto 4.3: Crea un programa que pida un número al usuario y diga si es positivo, negativo o cero.

Ejercicio de repaso propuesto 4.4: Haz un programa que pida al usuario dos números y diga cuántos de ellos son positivos.

Ejercicio de repaso propuesto 4.5: Crea un programa que pida al usuario dos números y muestre su división si el segundo no es cero, o un mensaje de aviso en caso contrario.

Ejercicio de repaso propuesto 4.6: Prepara un programa que pida al usuario tres números y diga cuál es el mayor de los tres.

Asignatura: Aplicaciones I

Curso: 4° Informática

Profesora: Evangelina Rivero

Actividades:

Chicos, se que muchos de ustedes están sin sus computadoras, es por eso que les mando la parte teórica, que es la explicamos en la Escuela para que ustedes puedan hacer un breve resumen. 

Lean con atención el material proporcionado. 

Los que tengan sus computadoras  o puedan realizar el trabajo en el celular realicen las actividades que les dejo al final.

Espero que pronto nos volvamos a encontrar!!

1) Leer la información y realizar un breve resumen en la carpeta. 

2) Realizar las actividades prácticas que están al final del texto.

Las tabulaciones en Word

Las tabulaciones te ayudan a alinear el texto una vez que has añadido una sangría o cuando quieres separar parte del texto en columnas. Por ejemplo, en tu hoja de vida debes escribir cuál es tu formación académica y especificar dónde y cuándo tomaste cada uno de los cursos. Para darle una presentación más profesional al documento, puedes alinear las fechas como en el siguiente ejemplo.

Selector de tabulación y tipos de tabulaciones:

El selector de tabulación está localizado al lado izquierdo de la panatalla, entre la regla vertical y la regla horizontal. Su función es permitirte seleccionar el tipo de tabulación que quieres usar en tu documento.

Al tabular puedes elegir:

• Tabulación izquierda: Te permite alinear la tabulación al lado izquierdo.

• Centrar tabulación: Centra el texto que se está tabulando.

• Tabulación derecha: Alinea el texto tabulado del lado derecho.

• Tabulación decimal: Alinea los números decimales.

• Barra de tabulación: Dibuja una línea vertical en el documento.

• Sangría de primera línea: Te permite insertar un marcador de sangría en la regla horizontal para alinear la primera línea de los párrafos del texto.

• Sangría francesa: Inserta un marcador de sangría francesa para alinear todas las líneas de los párrafos menos la primera.

Aunque en la Barra de tabulación, la Sangría primera línea y la Sangría francesa aparecen en el Selector de tabulación, estos no son precisamente tipos de tabulación.

Cómo añadir una tabulación:

Paso 1:

Selecciona el párrafo o los párrafos a los cuales quieres añadirles una tabulación.

Si no seleccionas algún párrafo, la tabulación se le aplicará al texto con el que estás trabajando y a los nuevos párrafos que crees.

Paso 2:

Haz clic en el Selector de tabulación hasta que aparezca el tipo de tabulación que quieres usar. En nuestro ejemplo usaremos la Tabulación derecha.

Paso 3:

En la regla horizontal, haz clic en el lugar donde quieras ubicar la tabulación. Si quieres ajustar muchos puntos de alineación de un mismo párrafo, lo puedes hacer.

Paso 4:

Ubica el Punto de inserción delante del texto que quieres tabular y presiona la tecla Tab de tu teclado. El texto se moverá hasta el lugar en el que hayas ubicado la tabulación en la regla.

Para remover un tabulación de la regla horizontal, arrástrala fuera de la regla.

Cómo insertar una imagen en Word

Word, procesador de texto que forma parte de la suite ofimática Microsoft Office, además de permitirte crear documentos de texto, te permite insertar imágenes para darles una mejor apariencia o resaltar cierta información. Existen diversas formas de agregar una imagen en Word, ya sea desde el menú Insertar, arrastrando la imagen o pegándola en el documento.

Cómo agregar una imagen en Word mediante la función 'Insertar'

Coloca el cursor donde quieras insertar la imagen y haz clic en la pestaña Insertar. En el grupo Ilustraciones, haz clic en una de las opciones, por ejemplo en Imágenes, selecciona la imagen que deseas añadir en tu PC y haz clic en Insertar:

Puedes cambiar el tamaño de la imagen usando los puntos que rodean la imagen, girarla moviendo la flecha circular o añadir efectos desde la pestaña Herramientas de imagen. Haz clic en Opciones de diseño y selecciona la alineación que mejor se acomode a tu documento para ajustar el texto alrededor de la imagen:

En el menú Insertar además dispones de otras opciones para insertar una imagen. Imágenes en línea te permite agregar una imagen de la web. Formas agrega una forma prediseñada como círculos, cuadrados y flechas. SmartArt inserta un elemento gráfico para comunicar información visualmente. Captura agrega una captura de pantalla.

Cómo insertar una imagen en Word arrastrando la imagen

Abre el Explorador de archivos y encuentra la imagen que quieras agregar. Haz clic sobre la imagen y arrástrala al documento Word. Suelta el botón del mouse para colocar la imagen en el lugar que desees.

Cómo añadir una imagen en Word mediante la función Copiar y Pegar

Encuentra la imagen que quieras insertar, ya sea en tu PC o en Internet, haz clic derecho sobre la imagen y selecciona Copiar. Luego, coloca el cursor donde quieras insertar la imagen, haz clic derecho y selecciona Pegar o presiona Ctrl + V

Aplicar una sangría en la primera línea de un párrafo

Para aplicar sangría a la primera línea de un párrafo, coloque el cursor al principio del párrafo y presione la tecla TAB. Al presionar entrar para iniciar el párrafo siguiente, se aplicará sangría a la primera línea.

Sugerencia: Si desea cambiar la sangría de párrafos que ya se han escrito, use el método de tecla de tabulación en el primer párrafo, como se describe anteriormente. Después coloque el cursor al principio del párrafo siguiente. Presione la tecla retroceso y, después, entrar. Repita el proceso para los párrafos subsiguientes.

Sangría de primera línea de forma predeterminada

Si desea usar siempre la sangría de la primera línea, modifique el estilo normal:

1. Coloque el cursor en cualquier lugar del párrafo.
2. En la pestaña Inicio , haga clic con el botón derecho en el estilo normal y elija modificar.
   
3. Seleccione formatoy, después, haga clic en párrafo.
   
4. En la pestaña sangría y espacio , en sangría, seleccione primera línea.
   
5. Seleccione Aceptar.
6. Vuelva a seleccionar Aceptar.
   Nota: Si siempre desea aplicar sangría de primera línea al iniciar un documento nuevo, elija la opción nuevos documentos basados en esta plantilla antes de seleccionar Aceptar.
   

Ejercicios para realizar en la computadora