Asignatura: Taller de Sistemas Operativos I

Curso: 4° Informática

Profesora: Evangelina Rivero

LOS SISTEMAS DE NUMERACIÓN A LO LARGO DE LA HISTORIA

Actividades

1) Leer el texto

2) Realizar una breve reseña o resumen da cada uno de los sistemas de numeración.

3) Mira los vídeos que están en el texto.

Cuando pensamos en matemáticas, a muchos nos da un gran dolor de cabeza, pero no debemos perder de vista la importancia de ellas y los avances que generaron en la sociedad y en las culturas de nuestros antepasados, teniendo gran importancia en el comercio, por ejemplo.

Los sistemas de numeración se inventaron por la necesidad de otorgar un símbolo a los objetos cuando queremos cuantificarlos o para saber su valor frente a un intercambio comercial, entre muchas cosas más. Con esta necesidad, las culturas antiguas buscaron la forma en representar esas cuentas por medio de símbolos que se traducen a una cantidad específica. De esta manera es como nacen los sistemas de numeración. Veamos algunos de ellos:

EGIPCIO (3000 A.C)

Un sistema decimal y aditivo.

Tres milenios antes de la era de Cristo, los egipcios ya contaban con el primer sistema desarrollado de numeración con  base 10 (contaban de diez en diez), por lo que cada símbolo lo podían repetir hasta nueve veces para poder utilizar el siguiente

Los números egipcios eran representados con diversos ideogramas.

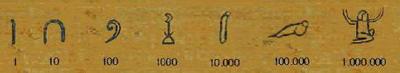
Ideogramas

Utilizaba el principio aditivo: había que sumar los valores de los numerales utilizados para escribir un número.

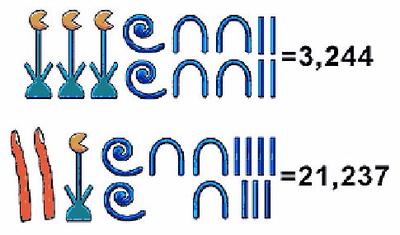
El orden en el que acomodaban  los símbolos no era importante, ya que cada símbolo tenía un único valor; es decir que su sistema de numeración no era posicional. Por ello no necesitaron el cero.

De esta manera, independientemente del orden en que éstos se presentaban, el valor no cambiaba.

La orientación para su escritura era indistinta: se podían escribir de izquierda a derecha, al revés o de arriba abajo, modificando la orientación de las figuras según el caso. Muchas veces esta disposición numérica variaba para lograr una mayor armonía estética, y solían ir acompañados de los jeroglíficos correspondientes al tipo de objeto cuyo número indicaban.

BABILÓNICO (1800-1900 A.C)

Un sistema sexagesimal

Este sistema apareció por primera vez alrededor de 1800-1900  a. C. También se acredita como el primer sistema de numeración posicional, es decir, en el cual el valor de un dígito particular depende tanto de su valor como de su posición en el número que se quiere representar.

Ideogramas

Para la unidad se usaba la marca vertical que se hacía con el punzón en forma de cuña. Se ponían tantos como fuera preciso hasta llegar a 10, que tenía su propio signo.

De este se usaban los que fuera necesario completando con las unidades hasta llegar a 60.

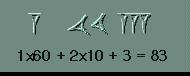
A partir del 60 se usaba un sistema posicional en el que los grupos de signos iban representando sucesivamente el número de unidades, 60, 60x60, 60x60x60 y asi sucesivamente.

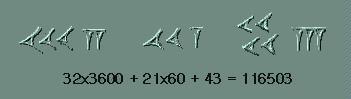
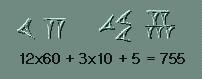
CHINO (1500 A.C)

Un sistema decimal y multiplicativo

La forma clásica de escritura de los números en China se empezó a usar desde el 1500 A.C. aproximadamente. Es un sistema decimal estricto que usa las unidades y los distintas potencias de 10. Usa la combinación de los números hasta el diez con la decena, centena, millar y decena de millar para según el principio multiplicativo representar 50, 700 ó 3000.  Los números chinos eran representados con diversos ideogramas.

ideogramas

Utilizaba el principio multiplicativo: primero el dígito (de 1 a 9), luego el lugar (10, 100...), y después el próximo dígito.El orden en el que acomodaban  los símbolos era fundamental, ya que 5 10 7 igual podría representar 57 que 75.

GRIEGO (600 A.C)

Sistema ático

El primer sistema de numeración griego se desarrolló hacia el 600 A.C. Era un sistema de base decimal que usaba los símbolos de la figura adjunta para representar esas cantidades. Se utilizaban tantas de ellas como fuera necesario según el principio de las numeraciones aditivas.

Para representar la unidad y los números hasta el 4 se usaban trazos verticales.

Para el 5, 10 y 100 usaban las letras correspondientes a la inicial de la palabra cinco (pénte), diez (déka), cien (hekatón), mil (khiloi), diez mil (myrías). Por este motivo se llama a este sistema acrofónico.

Los símbolos de 50, 500 y 5000 se obtienen añadiendo el signo de 10, 100 y 1000 al de 5, usando un principio multiplicativo.

Sistema ático

Sistema jónico

A partir del siglo V a. C., este sistema ático fue progresivamente reemplazado por el jónico que empleaba las 24 letras del alfabeto griego junto con algunos otros símbolos según la tabla adjunta.

A cada cifra de unidad (1 - 9) se le asigna una letra, a cada decena (10 - 90) otra letra y a cada centena (100 - 900) otra letra. Esto requiere 27 letras, así que se añadieron al sistema griego de 24 letras otras tres letras ya anticuadas:

. Stigma (ϛ) para el 6

. qoppa (ϙ) para el 90

. sampi (Ϡ) para el 900.

Sistema Jónico

ROMANO (27 A.C)

Durante todo el Imperio Romano se utilizó este sistema numérico, números romanos, que fue desarrollado en la antigua Roma y que todavía podemos ver en las fachadas de algunos edificios antiguos. Este sistema de numeración proviene del etrusco, ya que se han encontrado tallas antiguas que demuestran que los romanos cogieron os símbolos que utilizaban los etruscos para representar cantidades, y las adaptaron a su alfabeto.

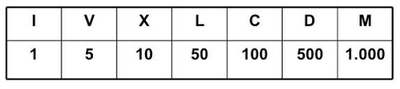
Sistema de numeración no posicional en el cual se emplean ideogramas simples, siete letras mayúsculas que cada una de ellas se corresponde con un valor numérico.

Para números con valores igual o superiores a 4000 se utiliza una rayita colocada encima de las letras e  indica tantos millares como unidades tenga este símbolo (Principio multiplicativo: se multiplica por 1000).

Si se colocan dos rayitas encima indican tantos millones como unidades tenga  el símbolo (se multiplica por 1 000,000)

MAYA ( 3 A.C)

Un sistema vigesimal

Los tres símbolos básicos eran el punto, cuyo valor es uno; la raya, cuyo valor es cinco; y el caracol (algunos autores lo describen como concha o semilla), cuyo valor es cero. Combinando estos símbolos se obtenían los números del 0 al 20. Es así como el sistema de numeración maya las cantidades son agrupadas de 20 en 20. De ahí que se lo llame sistema vigesimal porque está basado en el número 20.

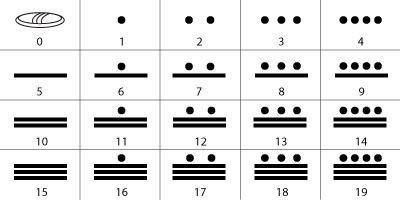
ideogramas

El sistema de numeración maya es posicional, se escribe de abajo hacia arriba, a diferencia del decimal que se escribe de izquierda a derecha.

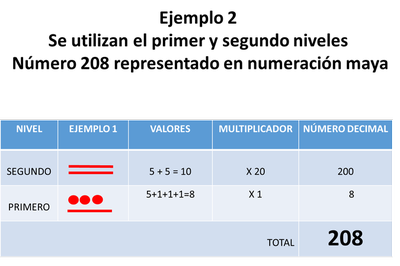
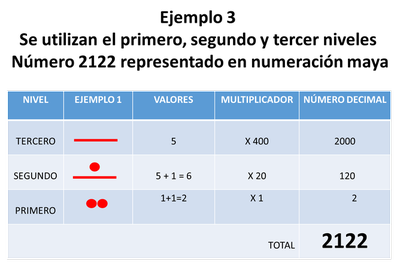
En el primer nivel van los símbolos que corresponden a los números del 0 al 19. Cuando se usa el primer nivel, el número ubicado en él se multiplica por 1 ya que el primer nivel equivale a la base a la cero potencia (b° = 1).

Cuando se usa el segundo nivel, el número ubicado en él se multiplica por 20 ya que el segundo nivel equivale a multiplicar por la base a la primera potencia (b¹ = 20).

Cuando se usa el tercer nivel, el número ubicado en él se multiplica por 400 ya que el tercer nivel equivale a multiplicar por la base a la segunda potencia (b² = 20 x 20 = 400)

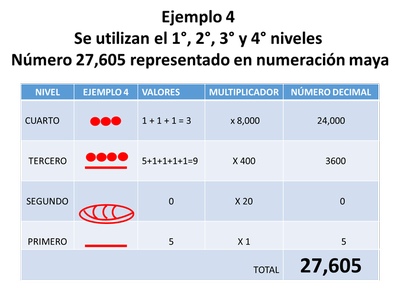
Cuando se usa el cuarto nivel, el número ahí ubicado se multiplica por 8000 ya que equivale a multiplicar por la base a la tercera potencia (b³ =20 x 20 x 20 = 8,000).

ACTUALIDAD

La numeración arábiga, que es como se denomina al sistema numérico que empleamos en la actualidad, nació en la India hacia el siglo V a.C. Fue allí donde se comenzó a contar del 1 al 10, como hacemos hoy.

De la India tomaron el sistema los árabes. En el año 825 Muhammad ibn Musa al-Khwarizmi publicó en Bagdad su tratado de álgebra.

Estos adelantos llegaron al resto de Europa a través de España hacia el siglo X, fecha en que viajó a Córdoba el monje francés Gerbert de Auvergnat, que en el 999 fue proclamado Papa con el nombre de Silvestre II. Fue el Papa que más contribuyó a difundir la nueva numeración, aunque tardó en imponerse.

La ciencia árabe, más avanzada que la cristiana en la Edad Media, no tardó en abrirse paso, y hacia 1200 Leonardo de Pisa escribió su Liber Abaci: la numeración de diez cifras estaba ya consagrada.

El sistema decimal, es un sistema de numeración posicional en el que las cantidades se representan utilizando como base aritmética  las potencias  del número diez. El conjunto de símbolos utilizado se compone de diez cifras